snake cube solver

Here is a picture of a wooden puzzle usually called a "Snake Cube." It is made up of 27 little blocks with an elastic cord running through all of them. There are 3 kinds of blocks: A straight block has the elastic enter through one face and exit through the opposite face; a corner block has the elastic enter through one face and exit through an adjacent face; and an end block has the elastic enter through one face but it does not exit.

I got a Snake Cube puzzle for Christmas but couldn't solve it. So I wrote a VB program to solve it and produce a printed solution. But then I began to wonder: How many different snake cube puzzles could possibly be built?

Of course, it is easy to see that there are 33,554,432 ways of constructing snakes: The 2 end blocks must be present at the ends and the remaining 25 blocks are made up of straight blocks and corner blocks. Since there are 2 ways to choose each of the 25 blocks, there are 2²⁵ = 33,554,432 possible combinations.

However, not every snake can be a cube. Obviously 25 straight blocks cannot form a cube (in fact, any snake with 2 straights together cannot form a 3x3x3 cube). How many of the 33 million or so snakes can be cubes?

I simply rewrote my puzzle solver and had it loop through all 33.5 million snakes, trying to find a solution for each one. I found 22,897 which could be solved (about 0.07%).

But how many different Snake Cubes are there? If you look at an example short snake you can see that E-C-C-S-E and E-S-C-C-E are the same snake. So at first glance it looks like my method of searching simply doubles the number of unique solutions. But what about palindromic snakes (ones that are the same forward and backward)? If any palindromic snakes are solvable, my program would count them only once.

So I again modified my program. If a snake is cubable, it now checks to see if it is also palindromic. Now it keeps track of how many total and how many palindromic solutions are found. So by counting the palindromic cubes and adding half the count of the remaining cubes (which are solved twice), we arrive at the total number of unique snake cubes = 11,487.

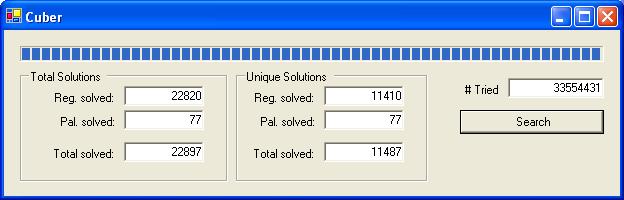
This confirms the number reported at Jaap's Puzzle Page. I'd like to thank Jaap, who took time out of his busy schedule to help troubleshoot my solving method.